The Mathematics of Music

The relationship between mathematics and music is often presented as an interesting coincidence. Here, we will explore the core of this relationship to understand not just that they are connected, but how and why this connection is so fundamental.

1. Ratios: The Architecture of Harmony

Our adventure begins in ancient Greece. Imagine a taut string (like on an ancient lyre). When you pluck it, it produces a tone. Pythagoras noticed that by pressing the string at specific points, the new sounds produced had a pleasant, harmonious relationship with the original. This relationship, he discovered, could be described with simple ratios of whole numbers.

Octave: The ratio 1:2 (half the string length)
Perfect Fifth: The ratio 2:3 (two-thirds of the string length)

But why do these simple ratios 'sound' good? The answer lies in the physics of waves. When the frequencies of two sounds have a simple ratio, their sound waves 'align' periodically, reinforcing each other in a way our brain perceives as consonant and pleasant. Harmony, ultimately, is a manifestation of mathematical order.

2. Rhythm and Fractions: Order Within Time

The same elegant logic of ratios we saw in pitch also applies to the duration of notes. The Pythagorean idea of harmony through numbers also runs through rhythm. Here, our tools are fractions.

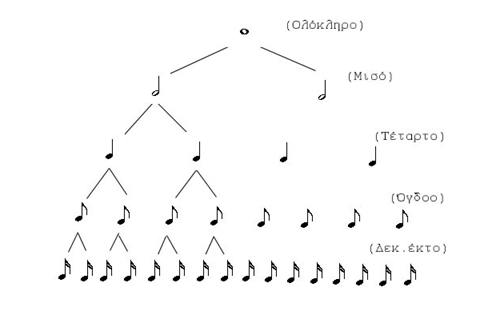
Think of a basic unit of time, the Whole Note (1). Every other note is a fraction of this unit:

Half Note: 1/2 of the Whole Note
Quarter Note: 1/4 of the Whole Note
Eighth Note: 1/8 of the Whole Note

The time signature, like 4/4, is the code that organizes musical time. Let's decode it: The numerator (the top 4) shows how many beats each measure contains. The denominator (the bottom 4) defines which note corresponds to each beat. Here, it's the 'quarter note' (1/4). So, 4/4 is a simple command: each measure is filled with notes totaling the value of 4 quarter notes. The musician doesn't do calculations but internalizes this rule, turning mathematical structure into a natural, rhythmic feeling. Thus, theory becomes a pulse that we feel.

3. The Sine Function: Describing Sound

How can we mathematically describe a sound? The answer lies in a function you know well from high school: the sine. The purest, simplest sound can be represented by a sine wave, which is described by the function:

y = A sin(Bx)

Let's decode this school function and turn it into music:

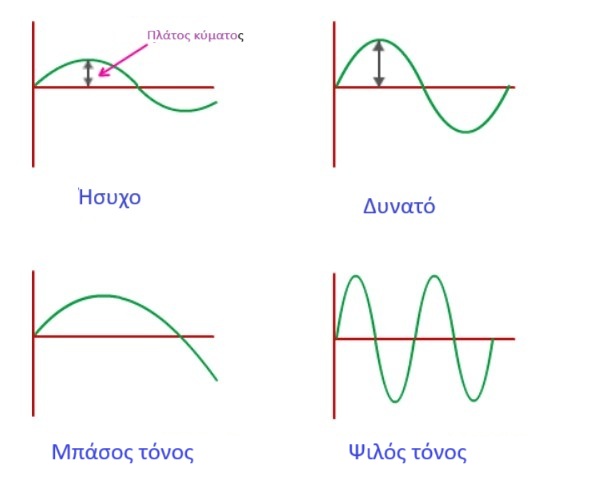
'A' (Amplitude) determines the Volume: 'A' is the height of the wave. The larger 'A' is, the louder the sound we hear.

'B' (Frequency) determines the Pitch: The 'B' parameter determines how 'dense' the waves are. When 'B' is large, the wave repeats quickly, producing a higher (acute) sound. When 'B' is small, the wave repeats slowly, producing a lower (bass) sound.

4. Timbre: The 'DNA' of Sound

But why do a piano and a guitar sound so different, even when playing the same note? The answer is timbre.

Musical instruments never produce a single, pure sine wave. What they produce is a complex wave, which consists of a strong sound at the fundamental frequency and a series of other, weaker sounds, called harmonics.

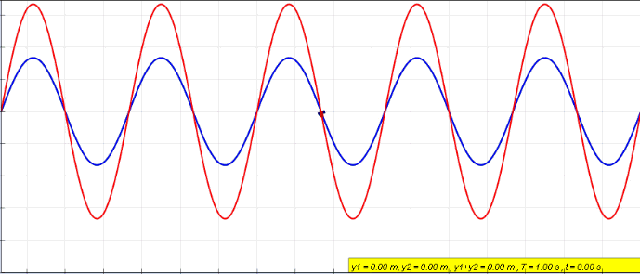
Each instrument emphasizes or weakens these harmonics in a unique way. This unique 'recipe' of each harmonic's intensity is the instrument's sonic DNA and the reason we can tell them apart.

Next Time in Math Class...

Remember, you're not just learning about fractions, sines, and functions. You're learning the fundamental building blocks of music! You're learning the grammar of music.