Ξεκλειδώστε τον Κώδικα: Πώς Δύο Αριθμοί δημιουργούν τον Ψηφιακό Κόσμο!

(Τα Μαθηματικά σας βοηθούν να Γίνετε Τεχνολογικός Υπερήρωας!)

Το Δυαδικό Σύστημα: Η Μυστική Γλώσσα των Υπολογιστών

Όταν κοιτάζετε την οθόνη του υπολογιστή σας, ένα βίντεο στο YouTube ή μια ταινία στη τηλεόραση βλέπετε μια εικόνα τόσο ζωντανή και πολύχρωμη που μοιάζει σχεδόν μαγική. Αλλά κάτω από αυτή την ψηφιακή επιφάνεια, όλα είναι χτισμένα από το πιο απλό δίδυμο που μπορείτε να φανταστείτε: τους αριθμούς 0 και 1.

Αυτό είναι το Δυαδικό Σύστημα, η μυστική γλώσσα των υπολογιστών.

Σκεφτείτε έναν διακόπτη φωτός: Είναι είτε ΚΛΕΙΣΤΟΣ (0) είτε ΑΝΟΙΧΤΟΣ (1). Δεν υπάρχει κάτι ενδιάμεσο. Οι υπολογιστές χρησιμοποιούν δισεκατομμύρια από αυτούς τους μικροσκοπικούς «διακόπτες» (τρανζίστορ) για να σκέφτονται, να θυμούνται και να αλληλεπιδρούν με τον κόσμο. Κάθε 0 ή 1 ονομάζεται bit.

Γιατί οι Υπολογιστές Χρησιμοποιούν Μόνο Δύο Αριθμούς;

Εμείς χρησιμοποιούμε το δεκαδικό σύστημα (βάση 10), πιθανότατα επειδή έχουμε δέκα δάχτυλα. Μας είναι οικείο και εύκολο στον υπολογισμό.

Αλλά για τις ηλεκτρονικές μηχανές, είναι πολύ πιο εύκολο και αξιόπιστο να καταλαβαίνουν αν το ηλεκτρικό ρεύμα απλώς ρέει (1) ή δεν ρέει (0). Φανταστείτε να προσπαθείτε να φτιάξετε έναν μικροσκοπικό διακόπτη που να αναγνωρίζει αξιόπιστα δέκα διαφορετικά επίπεδα «ενεργοποίησης» – θα ήταν εφιάλτης! Η απλότητα είναι το κλειδί για την ταχύτητα και την ακρίβεια στους υπολογιστές.

Η «Δύναμη» των Εκθετών: Μαθηματικά που Ήδη Ξέρετε!

Θυμάστε την αξία θέσης στα μαθηματικά; Στον αριθμό 345:

•  το 5 είναι στη θέση των μονάδων 5 x 100 = 5 x 1 = 5
•  το 4 είναι στη θέση των δεκάδων 4 x 101 = 4 x 10 = 40
•  το 3 είναι στη θέση των εκατοντάδων 3 x 102 = 3 x 100 = 300
   (Σύνολο= 300 + 40 + 5 = 345)

Το δυαδικό σύστημα χρησιμοποιεί ακριβώς την ίδια ιδέα, αλλά με δυνάμεις του 2 αντί του 10!

Ας αποκωδικοποιήσουμε τον δυαδικό αριθμό 1101:

•  Το ψηφίο τέρμα στα δεξιά είναι το 1 και αντιστοιχεί σε: 1 x 20 = 1 x 1 = 1
•  Το επόμενο ψηφίο είναι το 0 που αντιστοιχεί σε 0 x 21= 0 x 2 = 0
•  Το επόμενο 1:    1 x 22 = 1 x 4  = 4
•  Το αριστερότερο 1: 1 x 23= 1 x 8 = 8
   Προσθέστε τα: 8 + 4 + 0 + 1 = 13. Άρα, το δυαδικό 1101 είναι απλώς ο αριθμός 13 μεταμφιεσμένος!

Η Σημασία των Bits: Τι Μπορείς να Κάνεις με 0 και 1;

Γιατί είναι σημαντική αυτή η «δύναμη»; Ο αριθμός των bits (αυτά τα 0 ή 1) μας λέει πόσα διαφορετικά πράγματα μπορούμε να αναπαραστήσουμε.

•  1 bit έχει 21= 2 δυνατότητες (0, 1)
•  2 bits έχουν 22= 4 δυνατότητες (00, 01, 10, 11)
•  3 bits (23) έχουν 8 δυνατότητες (000, 001, ..., 111)
•  ...και φτάνουμε εδώ...
•  8 bits (ένα "byte") έχουν 28= 256 δυνατότητες!

256 δυνατότητες από μόλις οκτώ 0 και 1! Αυτό είναι αρκετό για να αναπαραστήσει κάθε γράμμα (Α-Ω, α-ω), κάθε αριθμό (0-9), όλα τα σημεία στίξης, και να περισσεύουν κιόλας κωδικοί! Αυτή είναι η μαγεία των εκθετών εν δράσει!

Από τα Δυαδικά Bits στις Οθόνες: Ζωγραφίζοντας με Αριθμούς!

Πώς λοιπόν το δυαδικό σύστημα μετατρέπεται στα εκπληκτικά γραφικά στην οθόνη σας;

• Η μαγεία των Pixels: Η οθόνη σας αποτελείται από εκατομμύρια μικροσκοπικές κουκκίδες που ονομάζονται pixels. Κάθε pixel είναι σαν ένα μικροσκοπικό, προγραμματιζόμενο φως.
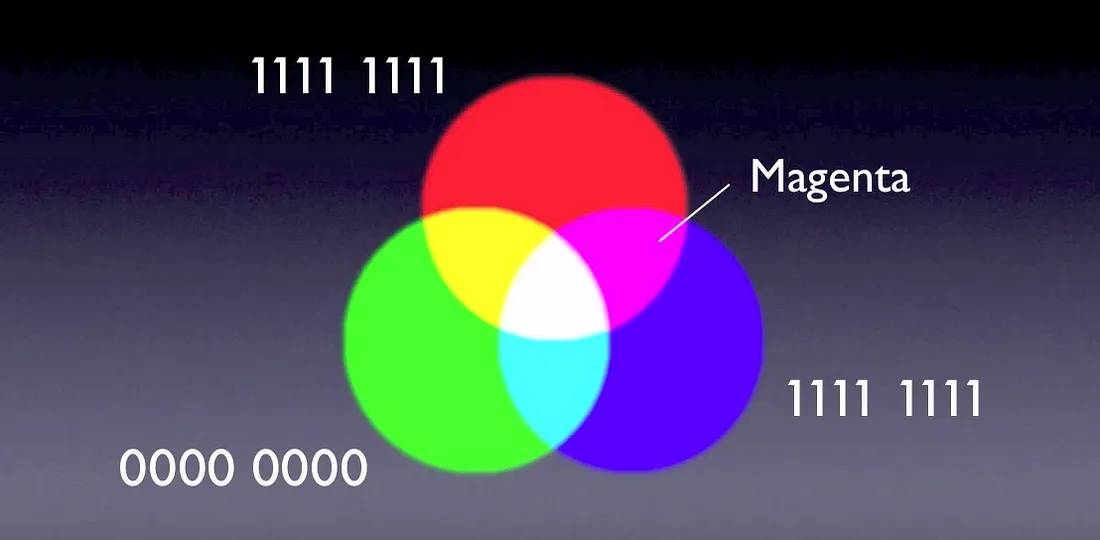
• Ο Κώδικας των Χρωμάτων (RGB): Κάθε pixel συνήθως έχει τρία ακόμη μικρότερα φώτα: Κόκκινο (Red), Πράσινο (Green), και Μπλε (Blue). Αλλάζοντας τη φωτεινότητα καθενός από αυτά τα τρία, ένα pixel μπορεί να εμφανίσει σχεδόν οποιοδήποτε χρώμα.
• Δυαδικό Σήμα για τη Φωτεινότητα: Πώς λέμε σε ένα μικροσκοπικό κόκκινο φως πόσο φωτεινό να είναι; Με το δυαδικό σύστημα, φυσικά! Συχνά, κάθε χρώμα (Κόκκινο, Πράσινο, Μπλε) παίρνει 8 bits πληροφορίας. • Το 00000000 (δυαδικό για το 0) θα μπορούσε να σημαίνει ότι το χρώμα είναι εντελώς ΚΛΕΙΣΤΟ. • Το 11111111 (δυαδικό για το 255) θα μπορούσε να σημαίνει ότι το χρώμα είναι σε ΠΛΗΡΗ ΦΩΤΕΙΝΟΤΗΤΑ. • Οποιοσδήποτε 8-bit αριθμός ενδιάμεσα (π.χ., 10000000 για μέτρια φωτεινότητα) δίνει μια διαφορετική απόχρωση!
• Εφόσον καθένα από τα R, G, και B μπορεί να έχει 2⁸ = 256 επίπεδα φωτεινότητας, ο συνολικός αριθμός χρωμάτων που μπορεί να εμφανίσει ένα pixel είναι 256 x 256 x 256 = 16,777,216 χρώματα! Αυτό είναι το «True Color», όλα από σειρές 0 και 1, με τη δύναμη των μαθηματικών των εκθετών!
• Η GPU: Ο Υπερ-Γρήγορος Καλλιτέχνης του Υπολογιστή σας: Η Μονάδα Επεξεργασίας Γραφικών (GPU) του υπολογιστή σας είναι ένα μαθηματικό τέρας! Παίρνει όλους αυτούς τους δυαδικούς κωδικούς για εκατομμύρια pixels και λέει σε καθένα τι χρώμα να είναι, ενημερώνοντάς τα πάρα πολλές φορές κάθε δευτερόλεπτο. Έτσι έχετε ομαλά βίντεο και γρήγορα παιχνίδια!

Το Δυαδικό Σύστημα: Η Παγκόσμια Γλώσσα του Υπολογιστή σου

Αυτό δεν αφορά μόνο τις οθόνες!

• Πληκτρολογείς ένα γράμμα; Το πληκτρολόγιό σου στέλνει έναν μοναδικό δυαδικό κωδικό για αυτό το γράμμα.
• Κάνεις κλικ με το ποντίκι σου; Δυαδικά σήματα λένε «κουμπί πατημένο» ή «κουμπί αφέθηκε».
• Ακούς μουσική; Το ψηφιακό αρχείο μουσικής είναι μια μεγάλη σειρά από δυαδικά ψηφία, που μετατρέπεται ξανά σε ηχητικά κύματα από ένα τσιπ που κάνει (το μαντέψατε) μαθηματικά!
• Τα πάντα που κάνει ο υπολογιστής σου, κάθε εφαρμογή, κάθε ιστοσελίδα, κάθε παιχνίδι, είναι τελικά ένας χορός από 0 και 1, που ερμηνεύονται χρησιμοποιώντας τους κανόνες των μαθηματικών που μαθαίνεις αυτή τη στιγμή.

Την Επόμενη Φορά στην Τάξη των Μαθηματικών...

Θυμήσου, δεν μαθαίνεις απλώς για εκθέτες, αξία θέσης ή λογική. Μαθαίνεις τα θεμελιώδη δομικά στοιχεία ολόκληρου του ψηφιακού κόσμου! Μαθαίνεις να μιλάς τη γλώσσα της τεχνολογίας.

Γι' αυτό τα μαθηματικά δεν είναι απλώς ένα μάθημα. Σου δίνουν την ικανότητα να κατανοείς, να δημιουργείς και να καινοτομείς σε έναν κόσμο που διαμορφώνεται όλο και περισσότερο από 0 και 1.