Τα Μαθηματικά της Μουσικής

Η σχέση μαθηματικών και μουσικής συχνά παρουσιάζεται σαν μια ενδιαφέρουσα σύμπτωση. Εδώ, θα εξερευνήσουμε τον πυρήνα αυτής της σχέσης για να καταλάβουμε ότι όχι απλώς συνδέονται, αλλά πώς και γιατί αυτή η σύνδεση είναι τόσο θεμελιώδης.

1. Οι Λόγοι: Η Αρχιτεκτονική της Αρμονίας

Η περιπέτειά μας ξεκινά από την αρχαία Ελλάδα. Φανταστείτε μια τεντωμένη χορδή (όπως σε μια αρχαία λύρα). Όταν τη χτυπάτε, παράγει έναν τόνο. Ο Πυθαγόρας παρατήρησε ότι πιέζοντας τη χορδή σε συγκεκριμένα σημεία, οι νέοι ήχοι που παράγονταν είχαν μια ευχάριστη, αρμονική σχέση με τον αρχικό. Αυτή η σχέση, όπως ανακάλυψε, μπορούσε να περιγραφεί με απλούς λόγους ακεραίων αριθμών.

Οκτάβα: Ο λόγος 1:2 (μισό μήκος χορδής)
Πέμπτη Καθαρή: Ο λόγος 2:3 (δύο τρίτα του μήκους της χορδής)

Γιατί όμως αυτοί οι απλοί λόγοι «ακούγονται» καλά; Η απάντηση βρίσκεται στη φυσική των κυμάτων. Όταν οι συχνότητες δύο ήχων έχουν έναν απλό λόγο, τα ηχητικά τους κύματα «ευθυγραμμίζονται» περιοδικά, ενισχύοντας το ένα το άλλο με έναν τρόπο που ο εγκέφαλός μας αντιλαμβάνεται ως σύμφωνο και ευχάριστο. Η αρμονία, τελικά, είναι μια εκδήλωση μαθηματικής τάξης.

2. Ο Ρυθμός και τα Κλάσματα: Η Τάξη μέσα στον Χρόνο

Η ίδια κομψή λογική των λόγων που είδαμε στον τονικό ύψος, εφαρμόζεται και στη διάρκεια των νοτών. Η πυθαγόρεια σκέψη της αρμονίας μέσω των αριθμών διατρέχει και τον ρυθμό. Εδώ, τα εργαλεία μας είναι τα κλάσματα.

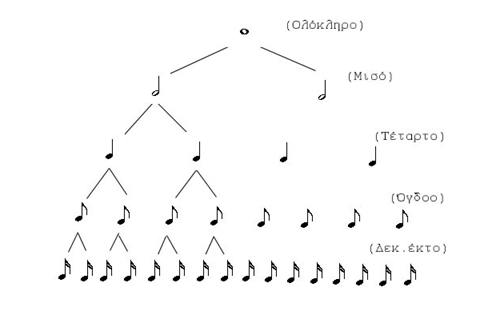
Σκεφτείτε μια βασική μονάδα χρόνου, το Ολόκληρο (1). Κάθε άλλη νότα είναι ένα κλάσμα αυτής της μονάδας:

Μισό: 1/2 του Ολοκλήρου
Τέταρτο: 1/4 του Ολοκλήρου
Όγδοο: 1/8 του Ολοκλήρου

Το μουσικό μέτρο, όπως το 4/4, είναι ο κώδικας που οργανώνει τον μουσικό χρόνο. Ας το αποκωδικοποιήσουμε: Ο αριθμητής (το πάνω 4) δείχνει πόσους χτύπους περιέχει κάθε μέτρο. Ο παρονομαστής (το κάτω 4) ορίζει ποια νότα αντιστοιχεί σε κάθε χτύπο. Εδώ, είναι το «τέταρτο» (1/4). Έτσι, το 4/4 είναι μια απλή εντολή: κάθε μέτρο γεμίζει με νότες συνολικής αξίας 4 τετάρτων. Ο μουσικός δεν κάνει υπολογισμούς, αλλά εσωτερικεύει αυτόν τον κανόνα, μετατρέποντας τη μαθηματική δομή σε μια φυσική, ρυθμική αίσθηση. Έτσι, η θεωρία γίνεται ένας παλμός που νιώθουμε.

3. Η Συνάρτηση Ημιτόνου: Περιγράφοντας τον Ήχο

Πώς μπορούμε να περιγράψουμε μαθηματικά έναν ήχο; Η απάντηση βρίσκεται σε μια συνάρτηση που γνωρίζετε καλά από το Λύκειο: το ημίτονο. Ο πιο καθαρός, απλός ήχος μπορεί να αναπαρασταθεί από ένα ημιτονοειδές κύμα, το οποίο περιγράφεται από τη συνάρτηση:

y = A ημ(Bx)

Ας αποκωδικοποιήσουμε αυτή τη σχολική συνάρτηση και ας τη μετατρέψουμε σε μουσική:

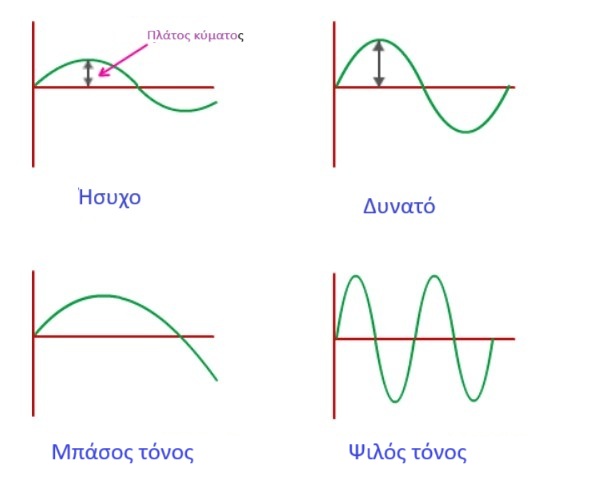
Το 'A' (Πλάτος) καθορίζει την Ένταση: Το 'Α' είναι το ύψος του κύματος. Όσο μεγαλύτερο είναι το 'Α', τόσο πιο δυνατός είναι ο ήχος που ακούμε.

Το 'B' (Συχνότητα) καθορίζει τον Τόνο: Η παράμετρος 'Β' καθορίζει πόσο 'πυκνά' είναι τα κύματα. Όταν το 'Β' είναι μεγάλο, το κύμα επαναλαμβάνεται γρήγορα, παράγοντας έναν πιο ψιλό (οξύ) ήχο. Όταν το 'Β' είναι μικρό, το κύμα επαναλαμβάνεται αργά, παράγοντας έναν πιο μπάσο ήχο.

4. Το Ηχόχρωμα (Timbre): Το «DNA» του Ήχου

Γιατί όμως ένα πιάνο και μια κιθάρα ακούγονται τόσο διαφορετικά, ακόμα κι όταν παίζουν την ίδια νότα; Η απάντηση είναι το ηχόχρωμα (timbre).

Τα μουσικά όργανα δεν παράγουν ποτέ ένα μόνο, καθαρό ημιτονοειδές κύμα. Αυτό που παράγουν είναι ένα σύνθετο κύμα, το οποίο αποτελείται από έναν ισχυρό ήχο στη βασική συχνότητα και μια σειρά από άλλους, πιο αδύναμους ήχους, που ονομάζονται αρμονικοί.

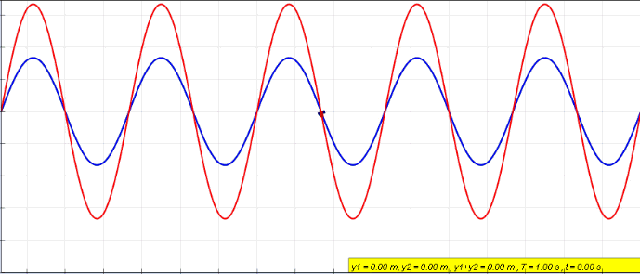
Κάθε όργανο τονίζει ή αποδυναμώνει αυτούς τους αρμονικούς με έναν μοναδικό τρόπο. Αυτή η μοναδική «συνταγή» της έντασης κάθε αρμονικού είναι το ηχητικό DNA του οργάνου και ο λόγος που τα ξεχωρίζουμε.

Την Επόμενη Φορά στην Τάξη των Μαθηματικών...

Θυμήσου, δεν μαθαίνεις απλώς για κλάσματα, ημίτονα και συναρτήσεις. Μαθαίνεις για τα θεμελιώδη δομικά στοιχεία της μουσικής! Μαθαίνεις τη γραμματική της μουσικής.