Η Τέχνη της Πρόβλεψης: Πώς τα Μαθηματικά Διαβάζουν το Μέλλον

Από την αρχαιότητα, οι άνθρωποι προσπαθούσαν να προβλέψουν το μέλλον. Κάποτε κοιτούσαμε τα άστρα ή ρωτούσαμε μαντεία. Σήμερα, έχουμε ένα πολύ πιο ισχυρό εργαλείο: την Ανάλυση Παλινδρόμησης (Regression Analysis). Αυτή είναι η μαθηματική μηχανή πίσω από τα πάντα, από τις προβλέψεις του χρηματιστηρίου μέχρι την Τεχνητή Νοημοσύνη. Είναι η τέχνη του να βρίσκεις την κρυφή σχέση μεταξύ αιτίας και αποτελέσματος.

Οπτικοποιώντας το Χάος

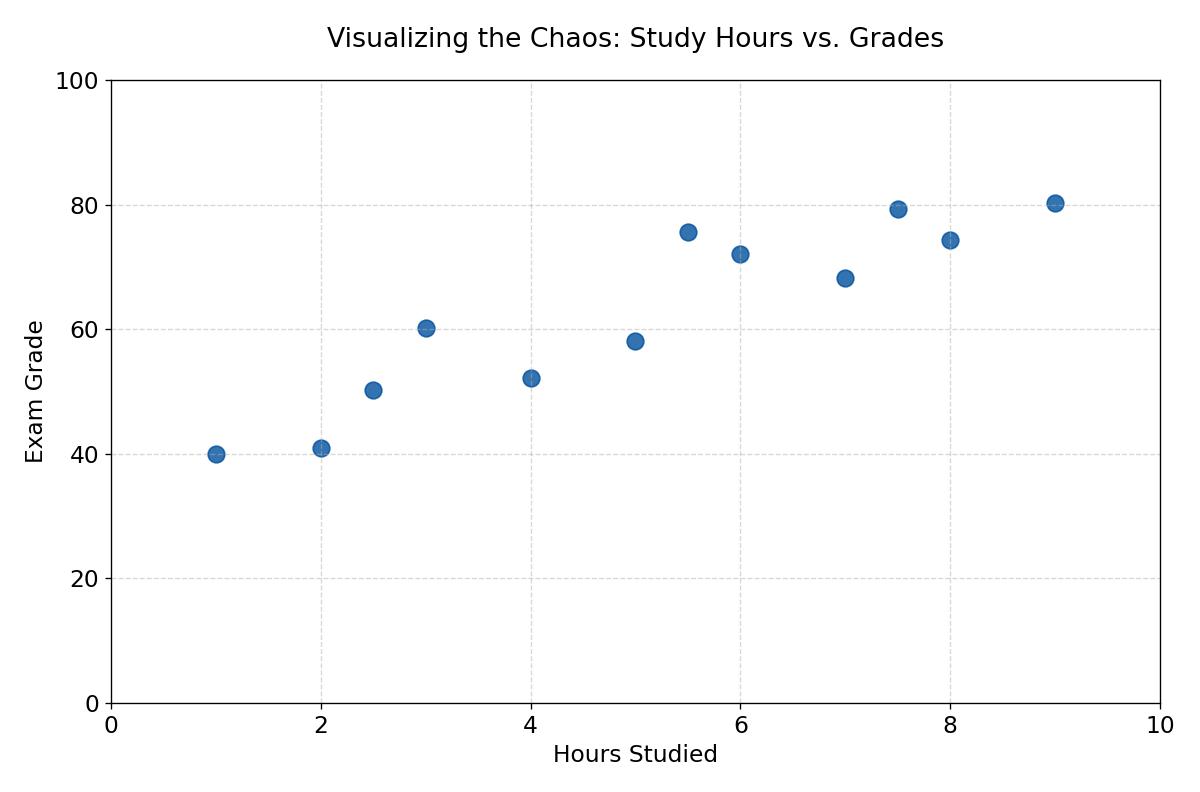
Φανταστείτε ότι θέλετε να απαντήσετε σε μια απλή ερώτηση: «Το περισσότερο διάβασμα φέρνει όντως καλύτερους βαθμούς;» Μπαίνετε σε μια τάξη και ρωτάτε 10 φοιτητές δύο πράγματα: πόσες ώρες διάβασαν και τι βαθμό πήραν.

Αν τοποθετήσετε αυτά τα σημεία σε ένα γράφημα, δεν θα πάρετε μια ευθεία γραμμή. Θα δείτε ένα «σύννεφο» από τελείες. Κάποιοι διάβασαν λίγο και στάθηκαν τυχεροί, άλλοι διάβασαν πολύ αλλά αγχώθηκαν. Αυτό το «σύννεφο» αντιπροσωπεύει το χάος του πραγματικού κόσμου. Για το άπειρο μάτι φαίνεται τυχαίο. Για έναν μαθηματικό, είναι ένας γρίφος που περιμένει τη λύση του.

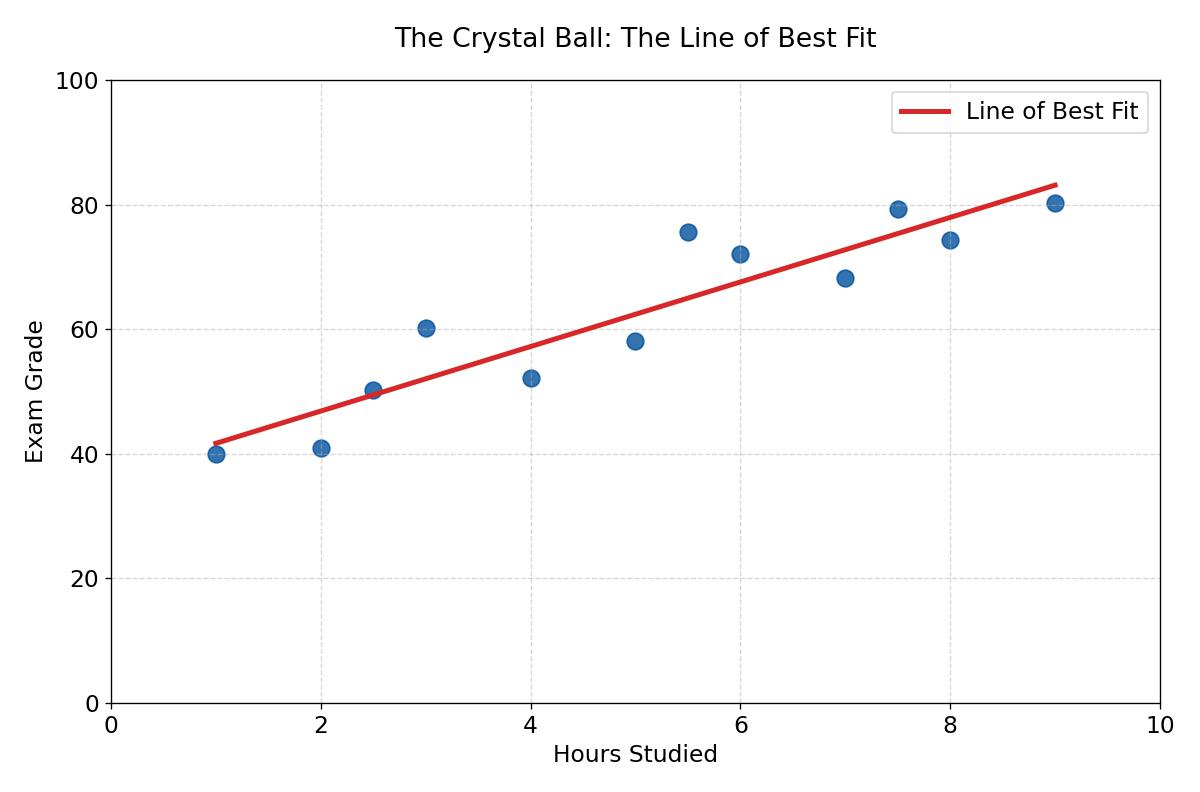
Η Κρυστάλλινη Σφαίρα: Η Ευθεία Βέλτιστης Προσαρμογής

Ο στόχος μας είναι να χαράξουμε μία και μοναδική ευθεία μέσα από αυτό το σύννεφο, η οποία να αντιπροσωπεύει την «τάση». Αυτή είναι η Ευθεία Βέλτιστης Προσαρμογής. Στο σχολείο τη γνωρίζετε ως:

y = α + βx   (η θεμελιώδης εξίσωση της Παλινδρόμησης)

Αυτή δεν είναι απλώς μια γραμμή. Είναι μια μηχανή πρόβλεψης. Μόλις έχουμε αυτή τη γραμμή, μπορούμε να κοιτάξουμε έναν φοιτητή που διάβασε 5 ώρες και να προβλέψουμε τον βαθμό του, ακόμα κι αν δεν τον έχουμε συναντήσει ποτέ. Η κλίση (το β) μας λέει τον μαγικό αριθμό: για κάθε επιπλέον ώρα διαβάσματος, πόσες μονάδες κερδίζεις;

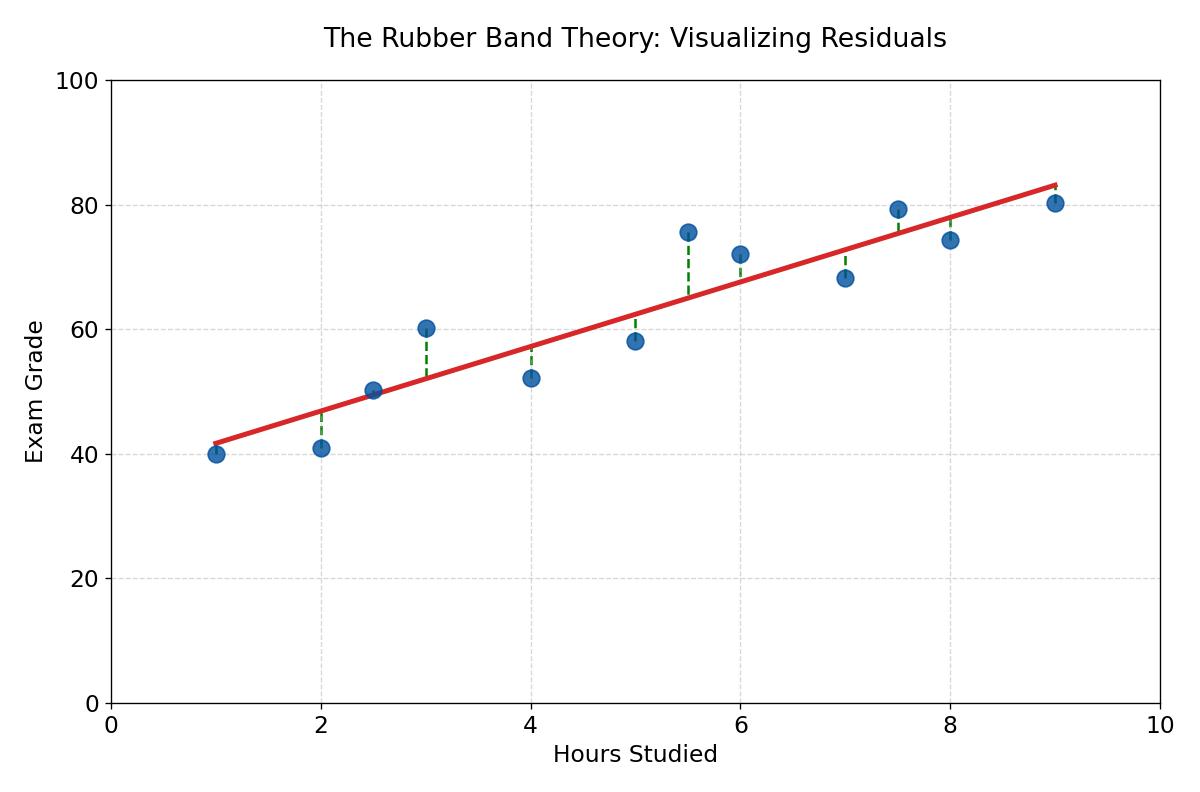
Η Θεωρία με τα Λαστιχάκια (Ελάχιστα Τετράγωνα)

Αλλά πώς επιλέγουμε πού ακριβώς θα μπει η γραμμή; Γιατί όχι λίγο πιο ψηλά; Λίγο πιο απότομα;

Φανταστείτε ότι κάθε τελεία στο γράφημα συνδέεται με τη γραμμή με ένα κάθετο λαστιχάκι. Οι τελείες τραβούν τη γραμμή προς το μέρος τους. Η γραμμή ισορροπεί ακριβώς εκεί που η ένταση από όλα τα λαστιχάκια εξισορροπείται.

Στα μαθηματικά, αυτό ονομάζεται Μέθοδος Ελαχίστων Τετραγώνων (OLS). Μετράμε την απόσταση κάθε τελείας από τη γραμμή (το «σφάλμα» ή «κατάλοιπο»), υψώνουμε αυτές τις αποστάσεις στο τετράγωνο και προσπαθούμε να κάνουμε το συνολικό άθροισμα όσο το δυνατόν μικρότερο. Η γραμμή που «αστοχεί» λιγότερο από όλες, είναι η νικήτρια.

Από τους Βαθμούς στη Wall Street

Αυτή η απλή ιδέα — το να χαράζεις μια γραμμή μέσα από δεδομένα — είναι το θεμέλιο της Οικονομετρίας. Έτσι προβλέπουν οι οικονομικοί διευθυντές τα έσοδα του επόμενου έτους. Έτσι εκτιμούν οι αλγόριθμοι την τιμή ενός ακινήτου με βάση τα τετραγωνικά του.

Ωστόσο, το πιο σημαντικό μάθημα στην παλινδρόμηση είναι το εξής: Η Συσχέτιση δεν συνεπάγεται Αιτιότητα (Correlation does not imply Causation). Ένας πραγματικός αναλυτής μαθαίνει να ερμηνεύει τα δεδομένα, όχι απλώς να τα υπολογίζει.

Η Δύναμη της Ανάλυσης

Η Ανάλυση Παλινδρόμησης είναι η γέφυρα μεταξύ των πρωτογενών δεδομένων και της γνώσης. Είτε είστε μαθητής IB που αναλύει ένα πείραμα φυσικής, είτε φοιτητής που χτίζει ένα χρηματοοικονομικό μοντέλο, η κατάκτηση αυτού του εργαλείου σάς δίνει τη δύναμη να βλέπετε τις αόρατες τάσεις που διαμορφώνουν τον κόσμο μας.